Martini 3 protein models - a practical introduction to different structure bias models and their comparison

If you would like to refer to information of this tutorial, please cite T. Duve, L. Wang, L. Borges-Araújo, S. J. Marrink, P. C. T. Souza, S. Thallmair, Martini 3 Protein Models - A Practical Introduction to Different Structure Bias Models and their Comparison, bioRxiv (2025), doi: 10.1101/2025.03.17.643608.

In case of issues, please contact duve@fias.uni-frankfurt.de, luis.borges@ens-lyon.fr, or thallmair@fias.uni-frankfurt.de.

Table of contents

Introduction

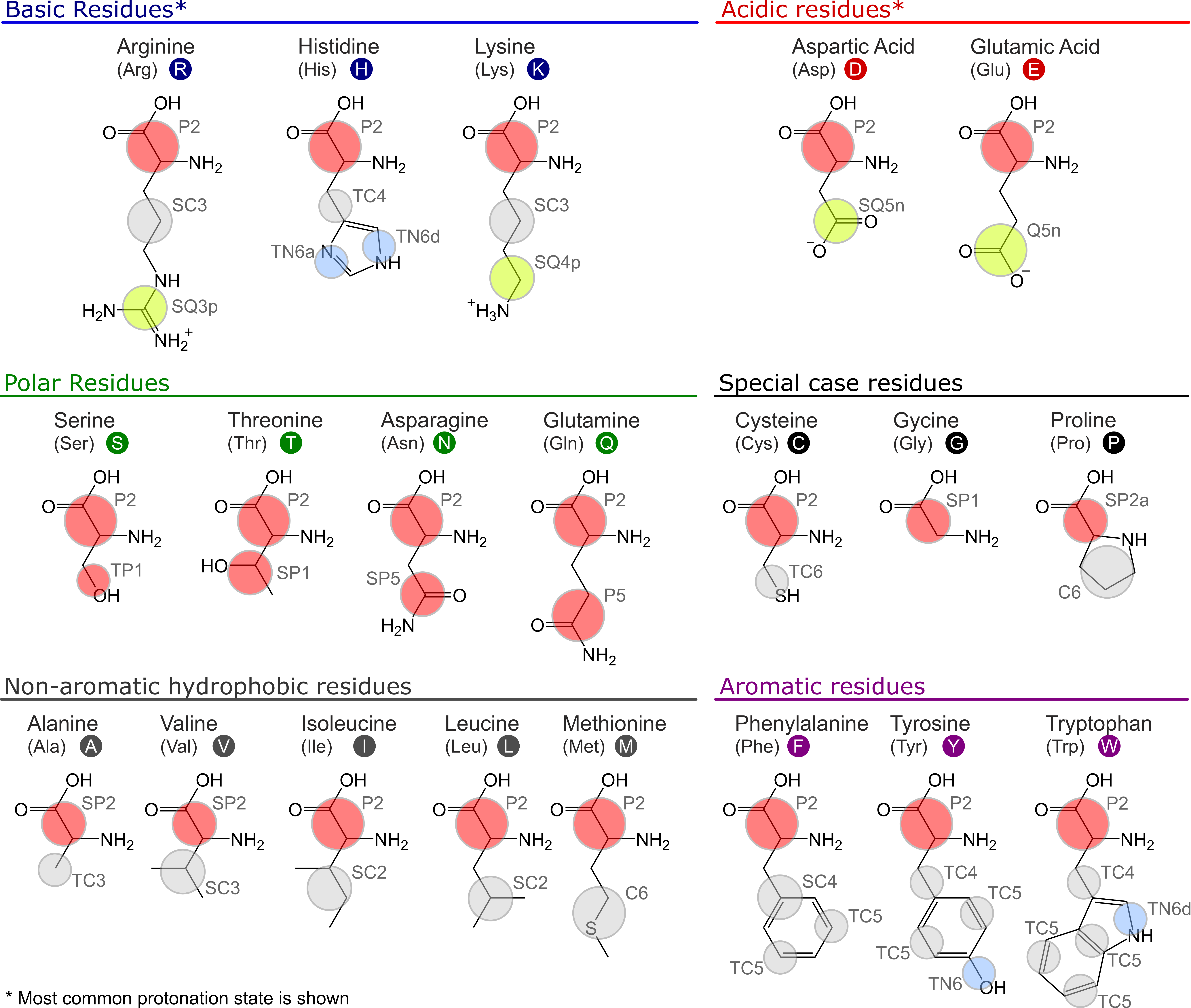
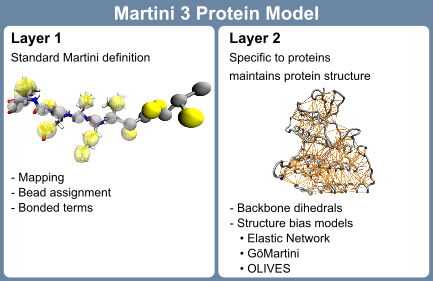
The Martini 3 protein model comprises two layers, which are strictly separated from each other: The first layer contains the mapping and chosen chemical bead types as well as the bonded terms; the second layer is the structure bias model. While the first layer corresponds to the standard definition of any molecule in the Martini universe, the second layer is more specific for proteins: To maintain the secondary, tertiary and quaternary structure of proteins, the directionality of interactions, in particular hydrogen bonds, are crucial. Due to the spherical potentials used in Martini 3 and many other CG force fields, this directionality is lost. Therefore, a structure bias model is required to stabilize protein structures. The strict separation between the two layers in Martini 3 enables independent development on both layers and is in contrast to the Martini 2 model[12], where mappings, bead types, and bonded terms were specific to each of the protein models. The first layer of the current Martini 3 protein model is mostly inherited from the Martini 2 model with moderate updates concerning the new mapping guidelines, bead types, and sizes. The Martini 3 mappings and bead types of the proteinogenic amino acids are depicted in Figure 1. A key difference to the previous model is that the bead type of the backbone (BB) bead does not depend on the secondary structure anymore but is represented by a P2 bead. Exceptions are the special cases glycine (SP1), alanine (SP2), valine (SP2), proline (SP2a), and terminal beads (Q5 for charged and P6 for neutral termini) [13].

Figure 1: Mapping and chemical bead types of amino acids in the Martini 3 protein model. The main classes of chemical bead types are indicated by color: P (polar, in red), N (intermediately polar, in blue), C (nonpolar, in gray), and Q (charged, in lime). Different bead sizes are indicated by the radius of the bead, with regular (no symbol), small (S), and tiny (T) beads.

Here, we will focus on the setup, fine-tuning options, and evaluation of the second layer of the Martini 3 protein model – the structure bias model – as well as on dedicated options for intrinsically disordered regions (IDRs). Overall, the Martini protein models require specific bonded terms to model the secondary structure [10, 12], which is in most cases combined with side-chain dihedral corrections [14]. In addition, there are three main options for structural bias models in layer 2 available, typically used to stabilize tertiary and quaternary structures, namely Elastic Network (EN) [3, 15, 16], GōMartini [13], and OLIVES [17] (Figure 2). Whereas the ad-hoc EN approach provides the most robust and straightforward way of stabilizing a protein structure, and has traditionally been used in Martini, the bioinformatics-based GōMartini approach is nowadays the method of choice as it has proven to be a more versatile method, striking a balance between protein stability and flexibility. Most recently, OLIVES was introduced as a physics-based variant of GōMartini, with the particular prospect of biasing quaternary structures as well.

Figure 2: Schematic visualization of the two-layered Martini 3 protein model.

In their simplest form, each of these three structure bias models relies on an atomistic reference structure which can be obtained from experiments or prediction software. The EN model uses harmonic potentials between the BB beads within a cutoff distance to maintain the protein structure. In contrast, both the GōMartini and OLIVES models employ Lennard-Jones potentials in a Gō-type manner, allowing for contact dissociation. In the GōMartini model, the potentials are defined from a contact map based on native contacts, evaluated through overlap and restricted contacts of structural units [18, 19], combined with a distance cutoff. The OLIVES model, on the other hand, defines its bias by evaluating the hydrogen bonding interactions between BB as well as side chain (SC) beads [17]. For small structured systems, such as single α-helices, the waiver of a structural bias model can be an option as well.

Tutorial Sections

The tutorial is structured as follows:

References

  1. Borges-Araújo L, Patmanidis I, Singh AP, et al (2023) Pragmatic Coarse-Graining of Proteins: Models and Applications. J Chem Theory Comput 19:7112–7135. https://doi.org/10.1021/acs.jctc.3c00733
  2. Samuel Russell PP, Alaeen S, Pogorelov TV (2023) In-Cell Dynamics: The Next Focus of All-Atom Simulations. J Phys Chem B 127:9863–9872. https://doi.org/10.1021/acs.jpcb.3c05166
  3. Souza PCT, Alessandri R, Barnoud J, et al (2021) Martini 3: a general purpose force field for coarse-grained molecular dynamics. Nat Methods 18:382–388. https://doi.org/10.1038/s41592-021-01098-3
  4. Abraham MJ, Murtola T, Schulz R, et al (2015) GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 1–2:19–25. https://doi.org/10.1016/j.softx.2015.06.001
  5. Lemkul JA (2024) Introductory Tutorials for Simulating Protein Dynamics with GROMACS. J Phys Chem B 128:9418–9435. https://doi.org/10.1021/acs.jpcb.4c04901
  6. Alessandri R, Barnoud J, Gertsen AS, et al (2022) Martini 3 Coarse-Grained Force Field: Small Molecules. Adv Theory Simul 5:2100391. https://doi.org/10.1002/adts.202100391
  7. Alessandri R, Thallmair S, Herrero CG, et al (2023) A Practical Introduction to Martini 3 and its Application to Protein-Ligand Binding Simulations. https://doi.org/10.1063/9780735425279_001
  8. Gil Herrero C, Thallmair S (2024) G-Protein-Coupled Receptor Surface Creates a Favorable Pathway for Membrane Permeation of Drug Molecules. J Phys Chem Lett 15:12643–12651. https://doi.org/10.1021/acs.jpclett.4c02875
  9. Pereira GP, Alessandri R, Domínguez M, et al (2024) Bartender: Martini 3 Bonded Terms via Quantum Mechanics-Based Molecular Dynamics. J Chem Theory Comput 20:5763–5773. https://doi.org/10.1021/acs.jctc.4c00275
  10. Borges-Araújo L, Pereira GP, Valério M, Souza PCT (2024) Assessing the Martini 3 protein model: A review of its path and potential. Biochim Biophys Acta BBA - Proteins Proteomics 1872:141014. https://doi.org/10.1016/j.bbapap.2024.141014
  11. Marrink SJ, Monticelli L, Melo MN, et al (2023) Two decades of Martini: Better beads, broader scope. WIREs Comput Mol Sci 13:e1620. https://doi.org/10.1002/wcms.1620
  12. Monticelli L, Kandasamy SK, Periole X, et al (2008) The MARTINI Coarse-Grained Force Field: Extension to Proteins. J Chem Theory Comput 4:819–834. https://doi.org/10.1021/ct700324x
  13. Souza PCT, Araujo LPB, Brasnett C, et al (2024) GōMartini 3: From large conformational changes in proteins to environmental bias corrections. 2024.04.15.589479
  14. Herzog FA, Braun L, Schoen I, Vogel V (2016) Improved Side Chain Dynamics in MARTINI Simulations of Protein–Lipid Interfaces. J Chem Theory Comput 12:2446–2458. https://doi.org/10.1021/acs.jctc.6b00122
  15. Kroon PC, Grunewald F, Barnoud J, et al (2024) Martinize2 and Vermouth: Unified Framework for Topology Generation. eLife 12:. https://doi.org/10.7554/eLife.90627.2
  16. Periole X, Cavalli M, Marrink S-J, Ceruso MA (2009) Combining an Elastic Network With a Coarse-Grained Molecular Force Field: Structure, Dynamics, and Intermolecular Recognition. J Chem Theory Comput 5:2531–2543. https://doi.org/10.1021/ct9002114
  17. Pedersen KB, Borges-Araújo L, Stange AD, et al (2024) OLIVES: A Go̅-like Model for Stabilizing Protein Structure via Hydrogen Bonding Native Contacts in the Martini 3 Coarse-Grained Force Field. J Chem Theory Comput 20:8049–8070. https://doi.org/10.1021/acs.jctc.4c00553
  18. Poma AB, Cieplak M, Theodorakis PE (2017) Combining the MARTINI and Structure-Based Coarse-Grained Approaches for the Molecular Dynamics Studies of Conformational Transitions in Proteins. J Chem Theory Comput 13:1366–1374. https://doi.org/10.1021/acs.jctc.6b00986
  19. Wołek K, Gómez-Sicilia À, Cieplak M (2015) Determination of contact maps in proteins: A combination of structural and chemical approaches. J Chem Phys 143:243105. https://doi.org/10.1063/1.4929599
  20. Grünewald F, Kroon PC, Souza PCT, Marrink SJ (2021) Protocol for Simulations of PEGylated Proteins with Martini 3. In: Chen YW, Yiu C-PB (eds) Structural Genomics: General Applications. Springer US, New York, NY, pp 315–335
  21. Ozturk TN, König M, Carpenter TS, et al (2024) Chapter Seven - Building complex membranes with Martini 3. In: Deserno M, Baumgart T (eds) Methods in Enzymology. Academic Press, pp 237–285
  22. Zeringo NA, Murphy L, McCloskey EA, et al (2013) A monoclinic crystal form of casein kinase 1 δ. Acta Crystallograph Sect F Struct Biol Cryst Commun 69:1077–1083. https://doi.org/10.1107/S1744309113023403
  23. Waterhouse A, Bertoni M, Bienert S, et al (2018) SWISS-MODEL: homology modelling of protein structures and complexes. Nucleic Acids Res 46:W296–W303. https://doi.org/10.1093/nar/gky427
  24. Abramson J, Adler J, Dunger J, et al (2024) Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 1–3. https://doi.org/10.1038/s41586-024-07487-w
  25. Anandakrishnan R, Aguilar B, Onufriev AV (2012) H++ 3.0: automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res 40:W537–W541. https://doi.org/10.1093/nar/gks375
  26. Olsson MHM, Søndergaard CR, Rostkowski M, Jensen JH (2011) PROPKA3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions. J Chem Theory Comput 7:525–537. https://doi.org/10.1021/ct100578z
  27. Lee J, Cheng X, Jo S, et al (2016) CHARMM-GUI Input Generator for NAMD, Gromacs, Amber, Openmm, and CHARMM/OpenMM Simulations using the CHARMM36 Additive Force Field. Biophys J 110:641a. https://doi.org/10.1016/j.bpj.2015.11.3431
  28. Jo S, Kim T, Iyer VG, Im W (2008) CHARMM‐GUI: A web‐based graphical user interface for CHARMM. J Comput Chem 29:1859–1865. https://doi.org/10.1002/jcc.20945
  29. Kabsch W, Sander C (1983) Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22:2577–2637. https://doi.org/10.1002/bip.360221211
  30. McGibbon RT, Beauchamp KA, Harrigan MP, et al (2015) MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys J 109:1528–1532. https://doi.org/10.1016/j.bpj.2015.08.015
  31. Alessandri R, Souza PCT, Thallmair S, et al (2019) Pitfalls of the Martini Model. J Chem Theory Comput 15:5448–5460. https://doi.org/10.1021/acs.jctc.9b00473
  32. Wassenaar TA, Ingólfsson HI, Böckmann RA, et al (2015) Computational Lipidomics with insane : A Versatile Tool for Generating Custom Membranes for Molecular Simulations. J Chem Theory Comput 11:2144–2155. https://doi.org/10.1021/acs.jctc.5b00209
  33. Andreasen MD, Souza PCT, Schiøtt B, Zuzic L (2024) Creating Coarse-Grained Systems with COBY: Towards Higher Accuracy in Membrane Complexity. 2024.07.23.604601
  34. Marrink S, Peter Tieleman D (2013) Perspective on the Martini model. Chem Soc Rev 42:6801–6822. https://doi.org/10.1039/C3CS60093A
  35. Souza PCT, Thallmair S, Marrink SJ, Mera-Adasme R (2019) An Allosteric Pathway in Copper, Zinc Superoxide Dismutase Unravels the Molecular Mechanism of the G93A Amyotrophic Lateral Sclerosis-Linked Mutation. J Phys Chem Lett 10:7740–7744. https://doi.org/10.1021/acs.jpclett.9b02868
  36. Thomasen FE, Pesce F, Roesgaard MA, et al (2022) Improving Martini 3 for Disordered and Multidomain Proteins. J Chem Theory Comput 18:2033–2041. https://doi.org/10.1021/acs.jctc.1c01042
  37. Larsen AH, Wang Y, Bottaro S, et al (2020) Combining molecular dynamics simulations with small-angle X-ray and neutron scattering data to study multi-domain proteins in solution. PLOS Comput Biol 16:e1007870. https://doi.org/10.1371/journal.pcbi.1007870
  38. Wang L, Brasnett C, Borges-Araújo L, et al (2024) Martini3-IDP: Improved Martini 3 Force Field for Disordered Proteins. submitted
  39. Grünewald F, Alessandri R, Kroon PC, et al (2022) Polyply; a python suite for facilitating simulations of macromolecules and nanomaterials. Nat Commun 13:68. https://doi.org/10.1038/s41467-021-27627-4
  40. Hilpert C, Beranger L, Souza PCT, et al (2023) Facilitating CG Simulations with MAD: The MArtini Database Server. J Chem Inf Model 63:702–710. https://doi.org/10.1021/acs.jcim.2c01375
  41. Yang S, Song C (2024) Multiple-Basin Gō-Martini for Investigating Conformational Transitions and Environmental Interactions of Proteins
  42. Eastman P, Galvelis R, Peláez RP, et al (2024) OpenMM 8: Molecular Dynamics Simulation with Machine Learning Potentials. J Phys Chem B 128:109–116. https://doi.org/10.1021/acs.jpcb.3c06662
  43. Yang S, Song C (2024) Switching Go̅-Martini for Investigating Protein Conformational Transitions and Associated Protein–Lipid Interactions. J Chem Theory Comput 20:2618–2629. https://doi.org/10.1021/acs.jctc.3c01222
  44. Korshunova K, Kiuru J, Liekkinen J, et al (2024) Martini 3 OliGo̅mers: A Scalable Approach for Multimers and Fibrils in GROMACS. J Chem Theory Comput 20:7635–7645. https://doi.org/10.1021/acs.jctc.4c00677
  45. Cofas-Vargas LF, Moreira RA, Poblete S, et al (2024) The Go-Martini Approach: Revisiting the Concept of Contact Maps and the Modelling of Protein Complexes. Acta Phys Pol ISSN 1898-794X 145:S9–S9. https://doi.org/10.12693/APhysPolA.145.S9
  46. Gomes DEB, Melo MCR, Gomes PSFC, Bernardi RC (2022) Bridging the gap between in vitro and in silico single-molecule force spectroscopy. 2022.07.14.500151
  47. Liu Z, Moreira RA, Dujmović A, et al (2022) Mapping Mechanostable Pulling Geometries of a Therapeutic Anticalin/CTLA-4 Protein Complex. Nano Lett 22:179–187. https://doi.org/10.1021/acs.nanolett.1c03584
  48. Humphrey W, Dalke A, Schulten K (1996) VMD: Visual molecular dynamics. J Mol Graph 14:33–38. https://doi.org/10.1016/0263-7855(96)00018-5
  49. Sami S, Grünewald F, Souza PCT, Marrink SJ (2023) A Guide to Titratable Martini Simulations. https://doi.org/10.1063/9780735425279_004
  50. Grünewald F, Souza PCT, Abdizadeh H, et al (2020) Titratable Martini model for constant pH simulations. J Chem Phys 153:024118. https://doi.org/10.1063/5.0014258
  51. Aho N, Buslaev P, Jansen A, et al (2022) Scalable Constant pH Molecular Dynamics in GROMACS. J Chem Theory Comput 18:6148–6160. https://doi.org/10.1021/acs.jctc.2c00516
  52. Chiariello MG, Grünewald F, Zarmiento-Garcia R, Marrink SJ (2023) pH-Dependent Conformational Switch Impacts Stability of the PsbS Dimer. J Phys Chem Lett 14:905–911. https://doi.org/10.1021/acs.jpclett.2c03760
  53. Claveras Cabezudo A, Athanasiou C, Tsengenes A, Wade RC (2023) Scaling Protein–Water Interactions in the Martini 3 Coarse-Grained Force Field to Simulate Transmembrane Helix Dimers in Different Lipid Environments. J Chem Theory Comput 19:2109–2119. https://doi.org/10.1021/acs.jctc.2c00950
  54. Spinti JK, Neiva Nunes F, Melo MN (2023) Room for improvement in the initial martini 3 parameterization of peptide interactions. Chem Phys Lett 819:140436. https://doi.org/10.1016/j.cplett.2023.140436
  55. Thomasen FE, Skaalum T, Kumar A, et al (2024) Rescaling protein-protein interactions improves Martini 3 for flexible proteins in solution. Nat Commun 15:6645. https://doi.org/10.1038/s41467-024-50647-9
  56. Zerze GH (2024) Optimizing the Martini 3 Force Field Reveals the Effects of the Intricate Balance between Protein–Water Interaction Strength and Salt Concentration on Biomolecular Condensate Formation. J Chem Theory Comput 20:1646–1655. https://doi.org/10.1021/acs.jctc.2c01273
  57. Koukos PI, Dehghani-Ghahnaviyeh S, Velez-Vega C, et al (2023) Martini 3 Force Field Parameters for Protein Lipidation Post-Translational Modifications. J Chem Theory Comput 19:8901–8918. https://doi.org/10.1021/acs.jctc.3c00604
  58. Atsmon-Raz Y, Tieleman DP (2017) Parameterization of Palmitoylated Cysteine, Farnesylated Cysteine, Geranylgeranylated Cysteine, and Myristoylated Glycine for the Martini Force Field. J Phys Chem B 121:11132–11143. https://doi.org/10.1021/acs.jpcb.7b10175
  59. Grünewald F, Punt MH, Jefferys EE, et al (2022) Martini 3 Coarse-Grained Force Field for Carbohydrates. J Chem Theory Comput 18:7555–7569. https://doi.org/10.1021/acs.jctc.2c00757
  60. Brandner AF, Smith IPS, Marrink SJ, et al (2025) Systematic Approach to Parametrization of Disaccharides for the Martini 3 Coarse-Grained Force Field. J Chem Inf Model. https://doi.org/10.1021/acs.jcim.4c01874
  61. Stevens JA, Grünewald F, Van Tilburg PAM, et al (2023) Molecular dynamics simulation of an entire cell. Front Chem 11:1106495. https://doi.org/10.3389/fchem.2023.1106495
  62. Pezeshkian W, Grünewald F, Narykov O, et al (2023) Molecular architecture and dynamics of SARS-CoV-2 envelope by integrative modeling. Structure 31:492-503.e7. https://doi.org/10.1016/j.str.2023.02.006
  63. Quemener E, Corvellec M (2013) SIDUS—the solution for extreme deduplication of an operating system. Linux J 2013:3