Parametrizing a new small molecule
- Details
- Last Updated: Sunday, 29 January 2023 02:15
Martini 3.0 tutorials: Parametrizing a new small molecule
!! Find the latest version of this tutorial FOLLOWING THIS LINK !!
Summary
1) Generate atomistic reference data
3) Generate the CG mapped trajectory from the atomistic simulation
4) Create the initial CG itp and tpr files
5) Generate target CG distributions from the CG mapped trajectory
7) Optimize CG bonded parameters
8) Comparison to experimental results, further refinements, and final considerations
Introduction
In this tutorial, we will discuss how to build a Martini 3.0 topology for a new small-molecule. The aim is to have a pragmatic description of the Martini 3.0 coar
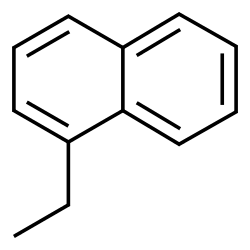
se-graining (CGing) principles described in Refs. [1] and [2], which follow the main ideas outlined in the seminal Martini 2 work [3]. Among other things, you may want to parametrize a small-molecule in order to perform protein-ligand binding simulations with Martini 3.0 [4]. The tutorial is based on the analogous Martini 2 tutorial, but takes into account a few important things which changed in Martini 3.0. We will use as an example the molecule 1-ethylnaphthalene, and make use of Gromacs versions 2019.x or later. Download here the archive containing the files which can help you go through this tutorial.
Note: This tutorial, now based on the Martini 3 open-beta version (v.3.0.b.3.2), will be updated as soon as the final parameters of Martini 3 are available (the paper is under review right now).
1) Generate atomistic reference data
We will need atomistic reference data to extract bonded parameters for the CG model. Note that we will need all the hydrogen atoms to extract bond lengths further down this tutorial, so make sure that your atomistic structure contains all the hydrogens.
Here, we will use the LigParGen server [5] as a way to obtain an atomistic (or all-atom, AA) structure and force field topology, but of course feel free to use your favorite atomistic force field. In this respect, an important option is to look in the literature for atomistic studies of the molecule you want to parametrize: if you are lucky, somebody published already a validated atomistic force field for the molecule and you can use such data and force field as reference material.
By feeding the SMILES string of 1-ethylnaphthalene (namely, CCc1cccc2ccccc21) to the LigParGen server, you will obtain a geometry (pdb) and OPLS-AA topology in Gromacs format (in this case, we picked the "1.14*CM1A-LBCC (Neutral molecules)" charges). Let's call them ENAP_LigParGen.pdb and ENAP_LigParGen.itp. You can now unzip the zip archive provided:
unzip martini3-tutorials--parametrize-sm-files-30b32.zip
which contains a folder called ENAP-in-water which contains some template folders and useful scripts. We will assume that you will be carrying out the tutorial using this folder structure and scripts. Note that the archive contains also a folder called ENAP-worked where you will find a worked version of the tutorial (trajectories not included). This might be useful to use as reference to compare your files (e.g., to compare the ENAP_LigParGen.itp you obtained with the one you find in ENAP-worked/1_AA-reference).
We can now move to the first subfolder, 1_AA-reference, move there the files you just obtained from the LigParGen server, and launch an atomistic molecular dynamics (MD) simulation:
cd ENAP-in-water/1_AA-reference
[move here the obtained ENAP_LigParGen.pdb and ENAP_LigParGen.itp files]
bash prepare_1mol_AA_system.sh ENAP_LigParGen.pdb spc216.gro SOL 3
The last command will run an energy-minimization, followed by an NPT equilibration of 250 ps, and by an MD run of 50 ns (inspect the script and the various mdp files to know more). In this case, the solvent used is water; however, the script can be adapted to run with any other solvent, provided that you input also an equilibrated solvent box. You should choose a solvent which represents the environment where the molecule will spend most of its time.
2) Atom-to-bead mapping
Mapping, i.e., splitting the molecule in building blocks to be described by CG beads, is the heart of coarse-graining and relies on experience, chemical knowledge, and trial-and-error. Here some guidelines you should follow when mapping a molecule to Martini 3.0 model:
- only non-hydrogen atoms are considered to define the mapping;
- avoid dividing specific chemical groups (e.g., amide or carboxylate) between two beads;
- respect the symmetry of the molecule; it is moreover desirable to retain as much as possible the volume and shape of the underlying AA structure;
- default option for 4-to-1, 3-to-1 and 2-to-1 mappings are regular (R), small (S), and tiny (T) beads; they are the default option for linear fragments, e.g., the two 4-to-1 segments in octane;
- R-beads are the best option in terms of computational performance, with the bead size reasonably good to represent 4-1 linear molecules;
- T-beads are especially suited to represent the flatness of aromatic rings;
- S-beads usually better mimic the “bulkier” shape of aliphatic rings;
- the number of beads should be optimized such that the maximum mismatch in mapping is ±1 non-hydrogen atom per 10 non-hydrogen atoms of the atomistic structure;
- fully branched fragments should usually use beads of smaller size (the rational being that the central atom of a branched group is buried, that is, it is not exposed to the environment, reducing its influence on the interactions); for example, a neopentane group contains 5 non-hydrogen atoms but, as it is fully branched, you can safely model it as a regular bead.
In this example, first of all it is important to realize that, within Martini 3.0, conjugated, atom-thick structures are best described by Tiny (T) beads. This ensures packing-related properties closely matching atomistic data [1,2]. In this case, the 10 carbon atoms of the naphthalene moiety are therefore mapped to 5 T-beads, as shown in the figure below:
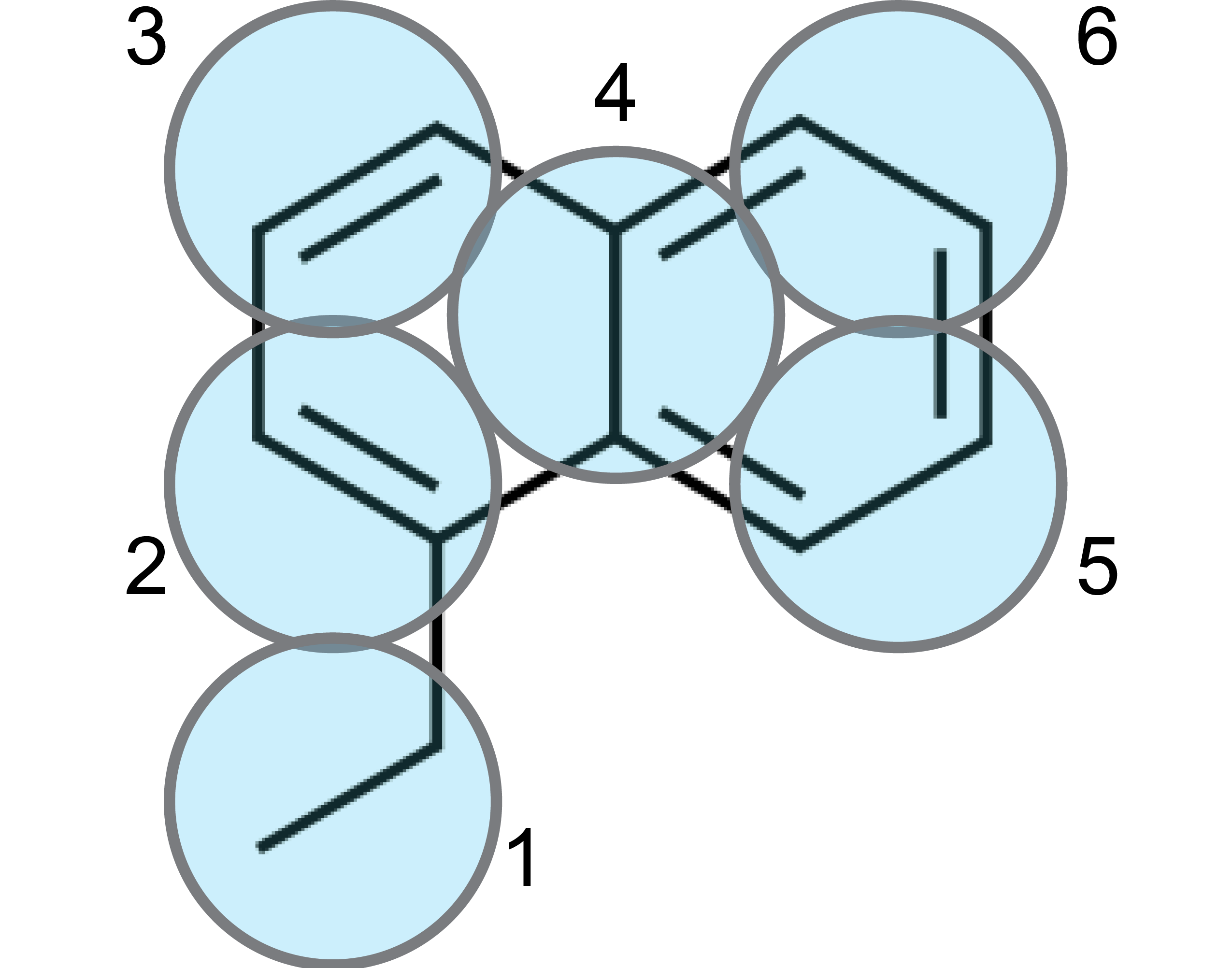
Which leaves us with the ethyl group. A T-bead is again a good choice because the T-bead size is suited for describing 2 non-hydrogen atoms. Note that, the beads have also been numbered in the figure for further reference.
A good idea to settle on a mapping is to draw your molecule a few times on a piece of paper, come up with several mappings, compare them, and choose the one that best fulfills the guidelines outlined above.
3) Generate the CG mapped trajectory from the atomistic simulation
Using the mapping you just created, you will now transform the simulation you did at 1) to CG resolution. One way to do this is by creating a Gromacs (AA-to-CG) index file where every index group stands for a bead and contains the mapped atom numbers.
Instead of creating an index file by hand from scratch, an initial AA-to-CG index file can be obtained with the CGbuilder tool [6]. The intuitive GUI allows to map a molecule on the virtual environment almost as one does on paper. Just load the atomistic pdb/gro file of the molecule, click on the atoms you want to be part of the first bead, click again to remove them if you change your mind, create the next bead by clicking on the "new bead" button, and so on; finally, download the files once done. In fact, the tool allows also to obtain an initial CG configuration (a gro file) for the beads and a CG-to-AA mapping file (a map file) based on the chosen mapping. Doesn't this sound better than traditional paper?! Current caveats of CGbuilder include the fact that atoms cannot contribute with a weight different from 1 to a certain bead, something which is sometimes needed when mapping atomistic structures to Martini. In such cases, the index and/or mapping files should be subsequently refined by hand.
Before you get to it: an important change with respect to Martini 2.x is the fact that now hydrogen atoms are taken into account to determine the relative position of the beads when mapping an atomistic structure to CG resolution [1,2] - more on this later in this Section. This should be reflected in your AA-to-CG index file, that is, your index should also contain the hydrogens (in CGbuilder terms, click also on the hydrogens!). The general rule is to map a certain hydrogen atom to the bead which contains the non-hydrogen atom it is attached to.
You can now try to map the ENAP_LigParGen.pdb via CGbuilder and compare the files obtained to the ones provided in ENAP-worked/2_atom-to-bead-mapping where, besides the files we just explained, you can also find a screenshot (ENAP_cgbuilder.png) of the mapping as done with the CGbuilder tool. Note also that the files provided assume the beads to be ordered in the same way as shown in the Figure of Section 2).
After having populated your own ENAP-in-water/2_atom-to-bead-mapping subfolder with - at least - the ndx file (let's call it ENAP_oplsaaTOcg_cgbuilder.ndx), move to the folder 3_mapped and copy over the index (we just rename it to mapping.ndx), that is:
cd ENAP-in-water/3_mapped
cp ../2_atom-to-bead-mapping/ENAP_oplsaaTOcg_cgbuilder.ndx mapping.ndx
Now, we took into account the hydrogens because center of geometry (COG)-based mapping of AA structures, done taking into account the hydrogen atoms, constitute the standard procedure for obtaining bonded parameters in Martini 3.0 [1,2]. Hence, we need to consider the hydrogens when mapping the AA structure to CG resolution. Because of a gmx traj unexpected behavior (a potential bug, see note [7]), if we want to stick to gmx traj (like in the good ol' days; alternatives include, e.g., using the MDAnalysis Python library), we need a little hack before being able to run gmx traj, namely we need to first create an AA tpr file with the atoms of the atomistic structure all having the same mass. To do this, still from the 3_mapped folder, create a new itp with the modified masses:
cp ../1_AA-reference/ENAP_LigParGen.itp ENAP_LigParGen_COG.itp
[Modify the file `ENAP_LigParGen_COG.itp` so that all atoms have *equal* mass (of, for example, `1.0`)]
and prepare a new top file which includes it:
cp ../1_AA-reference/system.top system_COG.top
sed -i 's/ENAP_LigParGen.itp/ENAP_LigParGen_COG.itp/' system_COG.top
You can now run the script:
bash 3_map_trajectory_COG.sh
which will:
- first make sure that the AA trajectory is whole, i.e., your molecule of interest is not split by the periodic boundary conditions in one or more frames in the trajectory file (the
gmx trjconv -pbc whole ...command); - subsequently create a
AA-COG.tpr, which will be used for the COG mapping in the following step (thegmx grompp -p ...command); - finally, map the AA trajectory to CG resolution: the
gmx traj -f...command contained in3_map_trajectory_COG.shwill do COG-mapping because it uses theAA-COG.tpr.
4) Create the initial CG itp and tpr files
The creation of the CG itp file has to be done by hand, although some copy-pasting from existing itp files might help to get the format right. The different directives you (probably) need are:
[ moleculetype ]: One line containing the molecule name and a number of exclusions. For Martini the standard number of exclusions is 1.[ atoms ]One line per atom, containing atomnumber, beadtype, residuenumber, residuename, atomname, chargegroup, charge, (mass). Residue number and residue name will be all the same for small molecules. Atomname can be freely chosen. In Martini every bead has its own charge group. Mass is usually not specified and in that case is taken from the bead definition.[ bonds ]One line per bond, containing atom 1, atom 2, function, average length, force constant. The functional form for Martini is 1. Bond length can be set to the average length obtained in step 5). The force constant should be adjusted to the width of the obtained histograms: small width means high force constant and vice versa (see also following Sections).[ constraints ],[ angles ],[ dihedrals ],[ exclusions ]- see the Gromacs manual for the right format.
Let's assume you call your initial CG itp file ENAP_initial.itp. Actually, you don't even need really to care about the bonded yet; have a look at the beginning of the next step (5)) for considerations about which bonded terms you will need.
Before going onto the next step, we need a CG tpr file to generate the distributions of the bonds, angles, and dihedrals from the mapped trajectory. To do this, move to the directory 4_initial-CG, where you should place the ENAP_initial.itp and that contains also a system_CG.top, the martini.itp and a martini.mdp and run the script:
cd 4_initial-CG
bash 4_create_CG_tpr.sh
The script will:
- extract one frame from your trajectory (mapping it of course);
- use the frame, along with the
topandmdp(see examples on the website) files to create aCG.tprfile for your molecule.
Following the “Martini 3.0 Bible” [1], you can also assign bead types based on the chemical building blocks. For a lengthier discussion of bead choices, see the final Section of this tutorial.
5) Generate target CG distributions from the CG mapped trajectory
We need to measure the length/angle of the bonded interactions (bonds, constraints, angles, proper and improper dihedrals) which we want in our CG model from our mapped-to-CG atomistic simulations from step 3). However, which bonded terms do we need to have? Let's go back to the drawing table and identify between which beads there should be bonded interactions.
5.1) On the choice of bonded terms for the CG model
The bonds connecting the T-beads within the 1-ethyl-naphthalene moiety are most likely going to be very stiff, that is, their distributions are going to be very narrow. This calls for the use of constraints [1,2,3]. A "naive" way of putting the model together would be to constrain all the beads (see Figure, left-hand side):
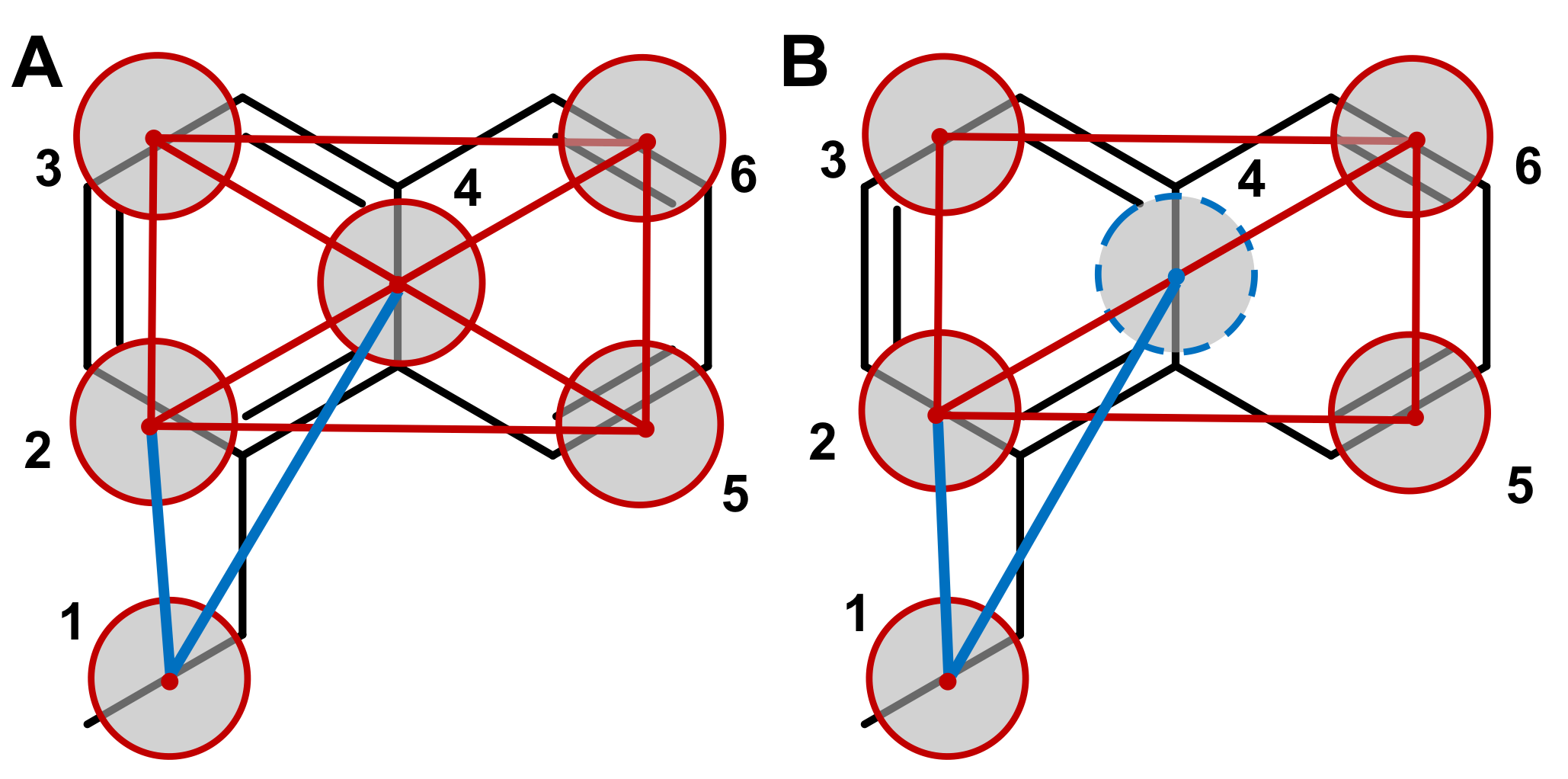
such a model, however, is prone to numerical instabilities, because it is increasingly complicated for the constraint algorithm to satisfy a growing number of connected constraints. Another option is to build a "hinge" model 2 where the 4 external beads (beads 2, 3, 5, and 6 of the Figure) are connected by 5 constraints to form a "hinge" construction, while the central bead (bead number 4) is described as a virtual site (VS), that is, a particle whose position is completely defined by its constructing particles (right-hand side of the Figure above). The use of virtual particles not only improves the numerical stability of the model but also improves performance [2]. As VSs are mass-less, the mass of the VS should be shared among the four constructing beads, so that beads 2, 3, 5, and 6 should have each a mass of 45 (= 36 + 36/4).
Bead 1 can then be connected by means of two bonds, namely 1-2 and 1-4. Two improper dihedrals (1-3-6-5 and 2-1-4-3) will be required in order to keep bead 1 on the right position onto the naphthalene ring. A final improper dihedral 2-3-6-5 will also be needed to keep the naphthalene ring flat. Exclusions between all beads should also be applied in this case, as the molecule is quite stiff and having intramolecular interactions in this case is not needed.
5.2) Index files and generation of target distributions
Once you have settled on the bonded terms, create index files for the bonds with a directive [bondX] for each bond, and which contains pairs of CG beads, for example:
[bond1]
1 2
[bond2]
1 4
...
and similarly for angles (with triples of CG beads) and dihedrals (with quartets). Write scripts that generate distributions for all bonds, angles, and dihedrals you are interested in. For 1-ethyl-naphthalene, there are seven bonds (5 constraints and 2 bonds) and three dihedrals, as discussed. A script is also provided, so that:
cd ENAP-in-water/5_target-distr
[create bonds.ndx and dihedrals.ndx]
bash 5_generate_target_distr.sh
will create the distributions. Inspect the folders bonds_mapped, and dihedrals_mapped for the results. You will find each bond distributions as bonds_mapped/distr_bond_X.xvg and a summary of the mean and standard deviations of the mapped bonds as bonds_mapped/data_bonds.txt.
For each bond, the script uses the following command (in this example, the command is applied for the first bond, whose index is 0):
echo 0 | gmx distance -f ../3_mapped/mapped.xtc -n bonds.ndx -s ../4_initial-CG/CG.tpr -oall bonds_mapped/bond_0.xvg -xvg none
gmx analyze -f bonds_mapped/bond_0.xvg -dist bonds_mapped/distr_bond_0.xvg -xvg none -bw 0.001
and similarly for the first dihedral:
echo 0 | gmx angle -type dihedral -f ../3_mapped/mapped.xtc -n dihedrals.ndx -ov dihedrals_mapped/dih_0.xvg
gmx analyze -f dihedrals_mapped/dih_0.xvg -dist dihedrals_mapped/distr_dih_0.xvg -xvg none -bw 1.0
6) Create the CG simulation
We can now finalize the first take on the CG model, ENAP_take1.itp, where we can use the info contained in the data_bonds.txt and data_dihedrals.txt files to come up with better guesses for the bonded parameters:
cd ENAP-in-water/6_CG-takeCURRENT
cp ../4_initial-CG/molecule.gro .
cp ../4_initial-CG/ENAP_initial.itp ENAP_take1.itp
[adjust ENAP_take1.itp with input from the previous step]
bash prepare_CG_1mol_system.sh molecule.gro box_CG_W_eq.gro W 1
where the command will run an energy-minimization, followed by an NPT equilibration, and by an MD run of 50 ns (inspect the script and the various mdp files to know more) for the Martini system in water.
Once the MD is run, you can use the index files generated for the mapped trajectory to generate the distributions of the CG trajectory:
cp ../5_target-distr/bonds.ndx .
cp ../5_target-distr/dihedrals.ndx .
bash 6_generate_CG_distr.sh
which will produce files as done by the 5_generate_target_distr.sh in the previous step but now for the CG trajectory.
7) Optimize CG bonded parameters
You can now plot the distributions against each other and compare. You can use the following scripts:
cd ENAP-in-water
gnuplot plot_bonds_tutorial_4x2.gnu
gnuplot plot_dihedrals_tutorial_4x1.gnu
The plots produced should look like the following, for bonds:
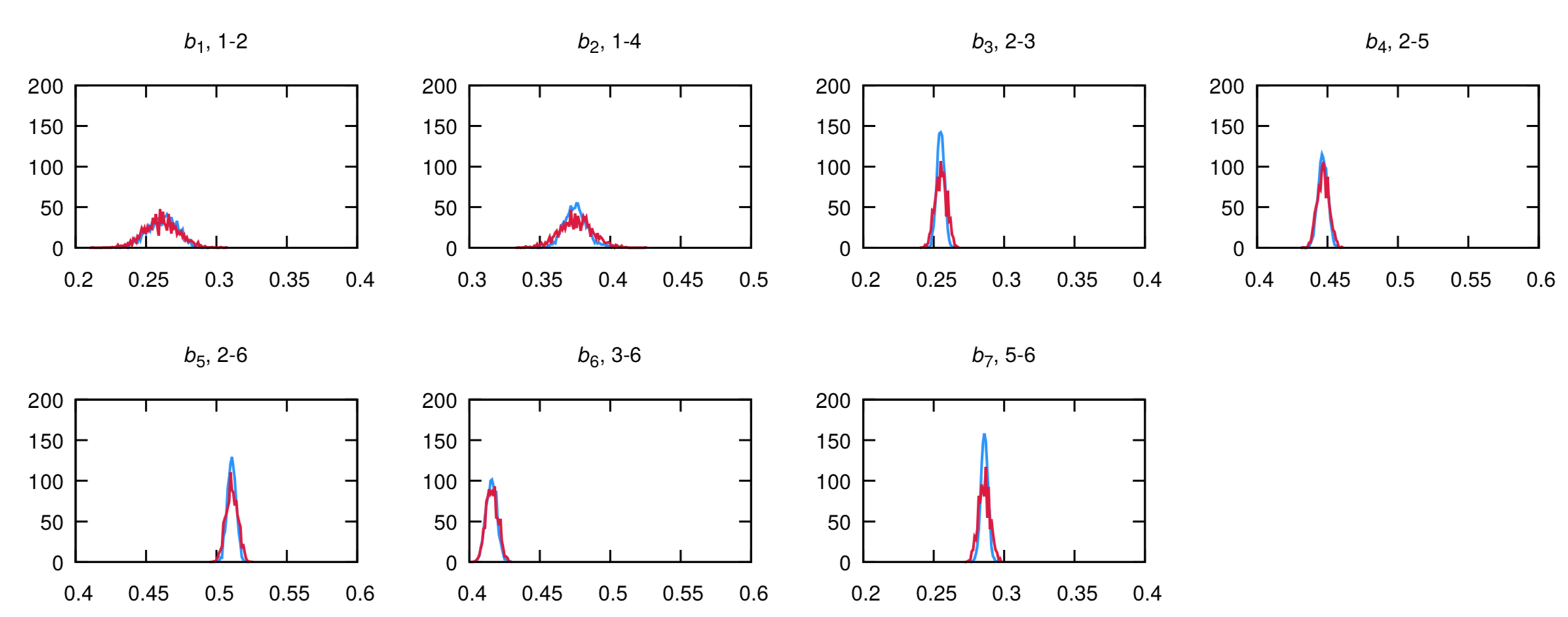
and dihedrals (AA is in blue, Martini is in red):

The agreement is very good. Note that the bimodality of the distributions of the first two dihedrals cannot be captured by the CG model. However, the size of the bead seemingly will capture the two configurations into a single one. If the agreement is not satisfactory at the first iteration - which is likely to happen - you should play with the equilibrium value and force constants in the CG itp and iterate till satisfactory agreement is achieved.
8) Comparison to experimental results, further refinements, and final considerations
8.1) Partitioning free energies
Partitioning free energies (see tutorial on how to compute them) constitute particularly good reference experimental data.
In the case of 1-ethyl-naphthalene, a model using 5 TC4 beads for the naphthalene double ring, and a TC2 bead for the ethyl group, leads to the following (excellent) agreement with available partitioning data (the experimental values are from Ref. [9]):
| logHD (kJ/mol) | logP (kJ/mol) | ||||
|---|---|---|---|---|---|
| Exp. | CG | Err. | Exp. | CG | Err. |
| 25.0 | 24.8 | -0.2 | 25.0 | 27.2 | 2.2 |
8.2) Molecular volume and shape
The approach described so far is oriented to high-throughput applications where this procedure could be automated. However, COG-based mappings cannot necessarily always work perfectly. In case packing and/or densities seem off, it is advisable to look into how the molecular volume and shape of the CG model compare to the ones of the underlying AA structure.
To this end, we can use the Gromacs tool gmx sasa to compute the solvent accessible surface area (SASA) and the Connolly surface of the AA and CG models. While AA force fields can use the default vdwradii.dat provided by Gromacs, for CG molecules, such file needs to be modified. For this, copy the vdwradii.dat file from the default location to the folder where we will execute the analysis:
cd ENAP-in-water/7_SASA
cp /usr/local/gromacs-VERSION/share/gromacs/top/vdwradii.dat vdwradii_CG.dat
The vdwradii.dat file in the current folder should now be edited so as to contain the radius of the Martini 3.0 beads based on the atomnames (!) of your system. By the way, the radii for the Martini R-, S-, and T-beads are 0.264, 0.225, and 0.185 nm, respectively (NOTE:: These are the values for the open-beta release, i.e., v.3.0.b.3.2; this value will change slightly in the final verison). Take a look at ENAP-worked/7_SASA/vdwradii.dat in case of doubts.
Now, run:
bash 7_compute_SASAs.sh ENAP
which will compute the SASA and Connolly surfaces for both the CG and AA models. The SASA will be computed along the trajectory, with a command that in the case of the AA model looks like this:
gmx sasa -f ../../3_mapped/AA-traj.whole.xtc -s ../../3_mapped/AA-COG.tpr -ndots 4800 -probe 0.185 -o SASA-AA.xvg
Note that the probe size is the size of a T-bead (the size of the probe does not matter but you must consistently use a certain size if you want to meaningfully compare the obtained SASA values), and the -ndots 4800 flag guarantees accurate SASA value. You will instead see that the command used to obtain the Connolly surface uses fewer points (-ndots 240) to ease the visualization with softwares such as VMD. Indeed, we can now overlap the Connolly surfaces (computed by the script on the energy-minimized AA structure and its mapped version) by using the following command:
vmd -m AA/ENAP-AA-min.gro AA/surf-AA.pdb CG/surf-CG.pdb
This should give you some of the views you find rendered below. Below you find also the plot of the distribution of the SASA along the trajectory - distr-SASA-AA.xvg and distr-SASA-CG.xvg (AA is in blue, Martini is in red):
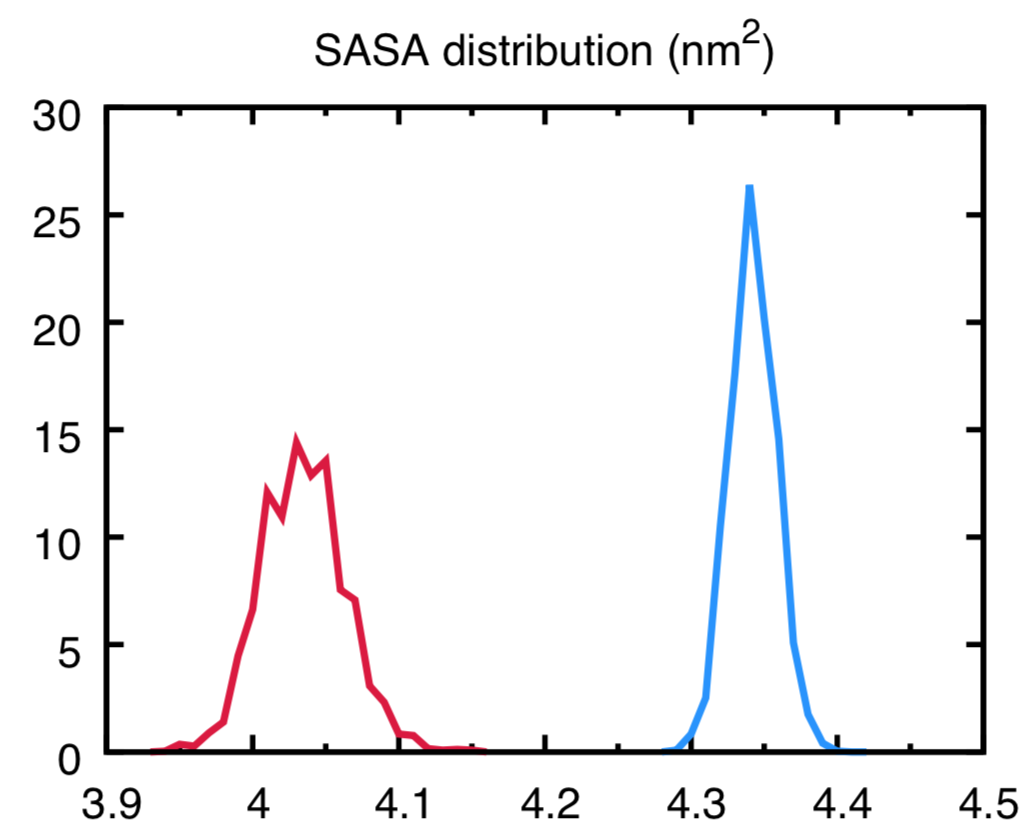
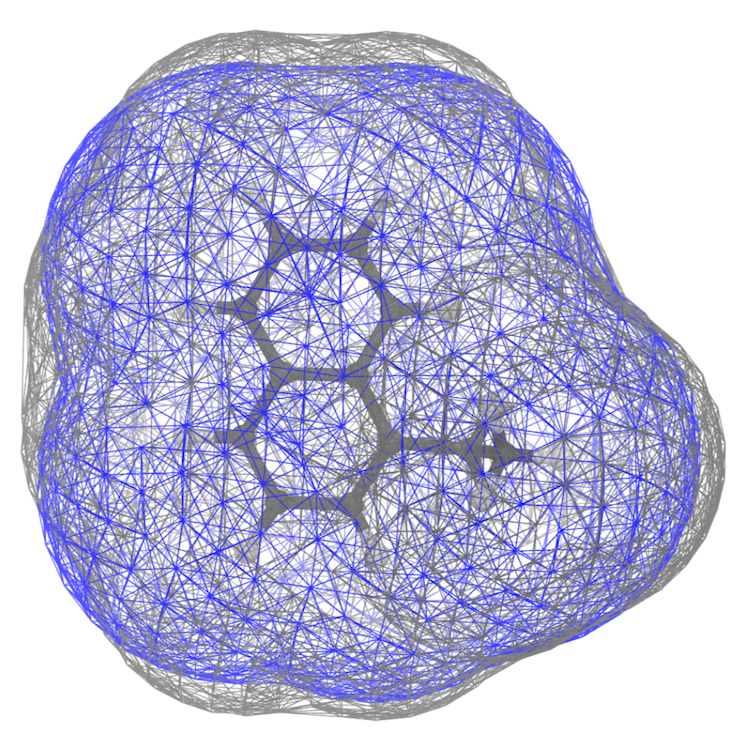

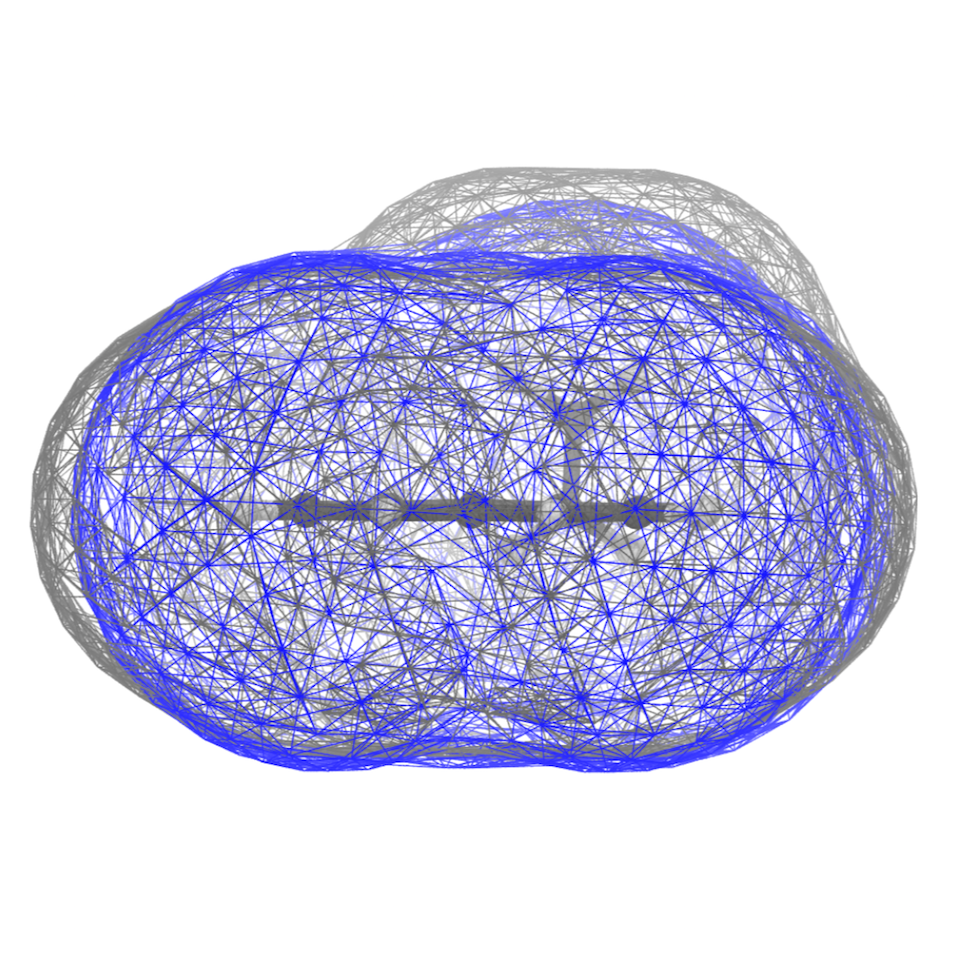
The SASA distributions show a discrepancy of about 7% (the average CG SASA is about 7% smaller than the AA one - see data_sasa_AA.xvg and distr-SASA-CG.xvg), which is acceptable (NOTE: The open-beta parameters tend to systematically underestimate the SASA; this is improved in the last version), but not ideal. Inspecting the Connolly surfaces (AA in gray, CG in blue) gives you a clearer picture: while the naphthalene moiety on average seems to be captured quite accurately by the CG model, the T-bead 1 does seem not to account for the whole molecular volume of the ethyl group. One way to improve this could be to lengthen bonds 1-2, and 1-4.
8.3) Final considerations
-
Mapping of some chemical groups, especially when done at higher resolutions (e.g., in aromatic rings), can vary based on the proximity of functional groups. The rule of thumb is that such perturbations may require a shift of ±1 in the degree of polarity of the bead in question.
-
Besides hydrogen bonding labels ("d" donor, and "a" for acceptor), electron polarizability labels are also made available in Martini 3.0 (NOTE: The latter labels are not available in the open-beta release, i.e., v.3.0.b.3.2): these mimic electron-rich (label "e") or electron-poor (label "v", for "vacancy") regions of aromatic rings. Such labels have been tested to a less extended degree than d/a labels, but have shown great potentials in applications involving aedamers [1]. In the case of 1-ethylnaphthalene, the "e" label may be used to describe bead number 4 (at the center of the naphthalene moiety) and bead number 2 (because connected to an electron-donating group such as -CH2CH3).
-
You may want to include other validation targets, besides free energies of transfer, depending on your application. Further useful reference experimental data include, for example, densities of pure liquids, or of organic crystals. More specific reference material can also be used: for example, for nucleobases we look at hydrogen-bonding strengths and specificity [1], following the Martini 2 DNA work [10].
References and notes
[1] P.C.T. Souza, et al., Martini 3.0: a General Purpose Force Field for Coarse-Grain Molecular Dynamics, to be submitted (2020).
[2] R. Alessandri, et al., Martini 3.0 Coarse-Grained Force Field: Ring Structures, to be submitted (2020).
[3] S.J. Marrink, et al., J. Phys. Chem. B. 2007, 111, 7812-7824.
[4] P.C.T.Souza, S. Thallmair, et al., Nat. Commun. 2020, 11, 3714.
[5] W.L. Jorgensen and J. Tirado-Rives, PNAS 2005, 102, 6665; L.S. Dodda, et al., J. Phys. Chem. B, 2017, 121, 3864; L.S. Dodda, et al., Nucleic Acids Res. 2017, 45, W331.
[6] J. Barnoud, https://jbarnoud.github.io/cgbuilder/cgbuilder.
[7] The Gromacs tool gmx traj won't allow to choose more than one group unless one passes the flag -com. Neither -nocom or omitting the flag altogether (which should give -nocom) work.
[8] M.N. Melo, H.I. Ingolfsson, S.J. Marrink, J. Chem. Phys. 2015, 143, 243152.
[9] S. Natesan, et al., J. Chem. Inf. Model. 2013, 53, 6, 1424-1435.
[10] J.J. Uusitalo, et al., J. Chem. Theory Comput. 2015, 11, 8, 3932-3945


























































































































































